Autómata finito no determinista (AFN)

Modelo matemático formado por:

-        Un conjunto de estados S

-        Un conjunto de símbolos de entrada ∑ (alfabeto de símbolos de entrada)

-        Una función de transición que transforma pares estado-símbolo en conjuntos de estados

-        Un estado s₀ que se considera el estado inicial

-        Un conjunto de estados  F considerados como estados de aceptación (estados finales)

 

 

Representación de los AFN

Se pueden representar mediante:

-        Grafos:

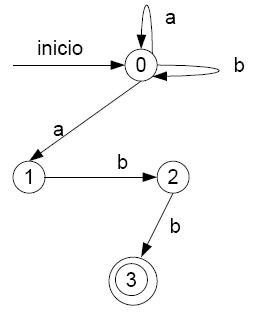
-        Tabla de transiciones:

 

 

 

 

Representación de expresiones regulares

mediante un AFD

-        Mediante un AFN puede reconocerse una expresión regular. Por ejemplo el autómata anterior permite reconocer el lenguaje de la expresión (a|b)*abb

-        En un AFN puede haber más de una secuencia de transiciones que conduzcan a un estado de aceptación.

 

 

Autómata finito determinista(AFD)

Es un AFN que cumple con las siguientes características:

-        Ningún estado tiene una transición con entrada épsilon

-        Para cada estado s y cada símbolo de entrada a, hay a lo sumo una arista etiquetada a que sale desde s.

 

Las transiciones de un AFD pueden representarse fácilmente mediante una matriz, como con los AFN.

 

 

Ejemplo de un AFD

 

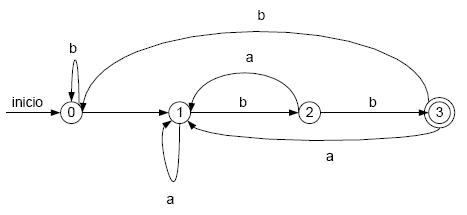
Conversión de un AFN a AFD

Algoritmo “construcción de subconjuntos”.

Se definen tres operaciones:

-        cerradura-ε(s): Conjunto de estados del AFN alcanzables desde el estado s con transiciones ε solamente.

-        cerradura-ε(T): Conjunto de estados del AFN alcanzables desde algún estado s del conjunto T con transiciones ε solamente.

-        mueve(T,a): Conjunto de estados del AFN hacia los cuales hay una transición con el símbolo de entrada a desde algún estado s en T del AFN.

 

Ejemplo

Con el siguiente AFN que equivale a la expresión (a|b)*abb

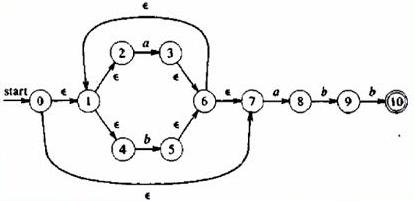
1. Llamaremos A al estado inicial del AFD y la cerradura- ε(0), con lo que A = {0,1,2,4,7}.

2. Como el alfabeto es {a,b} continuamos verificando para cuales estados de A hay transiciones con la letra a, en este caso 2 y 7 tienen hacia 3 y 8.

3. De ahí surge un nuevo estado B formado por {3,8} y cerradura-ε({3,8}), por lo que B = {1,2,3,4,6,7,8}.

4. Se realiza el paso 2 pero verificando transiciones con letra b, y surge el estado C ={5} + {1,2,4,6,7}

 

Ejemplo (cont)

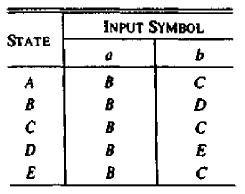
Realizando el mismo proceso con los nuevos estados que surjan y asignándoles una nueva letra, se llegarán a obtener cinco estados diferentes y la tabla que define el nuevo AFD

A = {0,1,2,4,7}

B = {1,2,3,4,6,7,8}

C = {1,2,4,5,6,7}

D = {1,2,4,5,6,7,9}

E = {1,2,4,5,6,7,10}